短期集中連載 超解説FIR! 最終回
短期集中連載
超解説FIR!
最終回
三村美照(M&Hラボラトリー)/兼子 紳一郎(ヤマハサウンドシステム) イラスト:あや

本誌特別企画「超解説FIR!」も本号で最終回を迎えます。前回まででFIRについて何となく理解していただけましたでしょうか? 最終回ではFIRを理解するのに最も重要でしかも難解な「畳み込み」の説明を中心にお送りします。また、それに関連してFIR-EQ/フィルターよりも早く畳み込みが応用された音響機器のお話を少し。最後にFIRの将来の展望に付いても触れたいと思います。
さて、前回にも書きました通りFIRの実態は「畳み込みをするための演算器」でした。ですから、これが分かればFIRは完璧?! では、早速進めていきましょう。
畳み込み?
皆さんの中には「畳み込み」という言葉を耳にしたことがあるという方、案外と多いのではないでしょうか。これも「FIR」を最近よく耳にするようになった影響でしょうか。「畳み込み」は計算方法の一種で正式には「畳み込み積分」といい、合成積や重畳積分と呼ばれることもあります。英語ではconvolution(コンボリューション)ですが、意外とこちらの英語の方がポピュラーかもしれませんね。

●
この畳み込みの概念の歴史は思いのほか古く、18世紀の半ば(!)頃にはその基礎ができていたと言われています。当時は何か実用的に利用するためというよりも、純粋に数学(微積分)の世界のお話で、ある定理を導き出すために用いた手段だったと記憶しています。世の中には頭の良い人がいるものですね。一方、私達の音響の世界では、20世紀の終わり1990年に入ってこの畳み込みを用いた機器が登場します。音響関係者であればこの機器のお世話になった方も多いと思いますが、このお話は後ほど…。
積分??
ここで「積分」という言葉が出てきました。実は前号にも出てきているのですが、その時はシレ~と流しましたが、今回は少しだけ説明します。
「積分」という言葉自体に何やら難しそうなイメージが…、名前だけは聞いたことがあるけどこの時点でもう無理…と思われた方も多いかと思います。
積分と対になる言葉に微分というものがあります。これらはニュートンの大発明(※1)とも呼ばれていますが、簡単にいうと物事がどのように変化するかを計算する方法で、「微分」はある微細な時間に変化する量(傾き)を導く方法、「積分」はある時間で変化した結果(面積や体積)を計算する方法と捉えれば、幾分かは分かり易いのではないでしょうか。次にもう少し具体的な例を説明します。
※1:「株式会社ニュートンプレス ニュートン」別冊「これなら分かるニュートンの大発明微分と積分」より引用
微積分をもう少し詳しく
例えば車が時速50km/hで1時間進むと50kmの距離を進みますよね。しかし実際のドライブにおいては車の速度は一定ではありませんからその時々の速度は異なります。最初の10分間の平均が30km/hであっても次の10分間は80km/hかもしれません。次にこの10分間という間隔を更に短くして1分間隔、1秒間隔…としていくと、非常に短い時間での平均速度になります。更にもっと細かく見ていくと、ある瞬間々々の速度となります。これを「ある距離の間を時間で微分するとその時の速度が分かる」と言います。
次に、この車は動いていますので短い時間であってもある距離を進みますから、10分間隔の平均速度が分かりそれら6個を合計すれば1時間で進んだ距離が計算できます。この時、より正確に距離を求めようとすると10分間隔よりも1分間隔の平均速度を60個足した方が正確な距離を求めることができます。また1秒、0.1秒…と更に細かくすればするほどより正確に進んだ距離を求めることができます。このようにその時々の速度が分かればその時間に進んだ距離が分かりますので、それらを足し算すれば全体で進んだ距離が計算できます。この計算方法を積分と言い、これを「速度を時間で積分すれば距離が分かる」と言います。これをグラフにしてみると、微分はある時間のグラフの傾きになり、積分はある時間範囲の面積となります。この面積は別の言い方をすると、ある時間範囲で「変化した結果」と捉えることができます。
では畳み込み積分はというと、別名で“合成積や重畳積分”とも呼ばれると言いましたが、この名前から2つの物事を合成し、更に「積分」の文字が付いているので「2つの物事がある時間で合体して変化した結果」を計算する方法だということになります。そして今回の場合の2つの物事とは、音声信号とIR(インパルスレスポンス)のことです。
畳み込みとは
ではいよいよ畳み込みがどのようなものか、具体的に説明していきましょう。
いま2つの関数G(t)とH(t)があるとします。今度は「関数」という言葉が出てきて又々拒絶反応が起こりそうなイメージですが、単に時間によって変化する「値」と思ってください。変化していますからその値を辿っていくとある形になりますよね。その「時間的な変化を伴う値」を「関数」というもので表現しています。このGやHの後ろに(t)という文字が付いているのは時間と共に変化するという意味です。つまり、図1-(1)のG(t)とH(t)ように横軸が時間で縦軸が大きさで表されます。ここまでは皆さんもお分かりですね。
このうちG(t)は少し特殊な関数で、時間に関する関数でありながらそれ自体が時間と共に平行移動する関数です。関数というと難しく聞こえますので「形」と言い換えても良いでしょう。つまりG(t)はその形のまま時間と共に平行移動します。先程の図で四角形の部分にあたります。
ここでこの2つの関数、つまり一方は固定しもう一方は時間と共に移動するものを合体(畳み込み)させてみましょう。この時の合体は数学的な掛け算と足し算が行なわれます(「重ね足し合わせ」と言う)。もう少し詳しく言うと2つの関数が重なっている部分の中で、Y軸上にある値同士を掛け算してそれらをすべて足し合わせます。では、その結果はどうなるでしょうか? 各図下部の太線が畳み込まれた結果です。
同図を順に見ていくと、(2)ではG(t)が右に進んでいくとH(t)と重なっていますが、重なっている中で斜線を引いた部分の面積が各時間における畳み込まれた結果で、時間と共に斜線部分が変化することがお分かり頂けると思います。実際にそれぞれ斜線の面積を計算して、移動している四角形の先頭の位置にその値をプロットして見てください。図のような形になることが分かります。固定した三角形と移動する四角形を畳み込むとこのような形になるのですね!
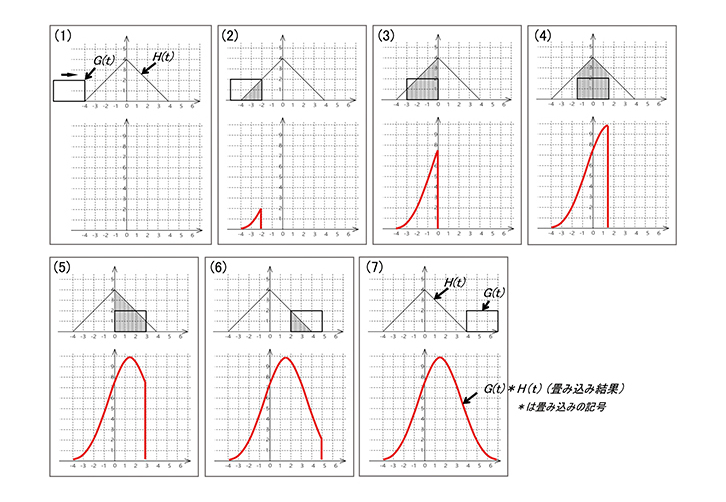
図1 畳み込みの概念
固定している三角形に移動する四角形を畳み込むと下の太線のようになる
デジタルデータの畳み込み
ところで、この図形の線は(時間的に)連続しているのでアナログ的な図です。一方、今回扱うのはデジタルデータです。ご存知の通りデジタルデータは連続していません。ある時間の間隔で独立しています。これを連続しているアナログデータに対して離散データ(Discrete Data)と呼びます。
ではこの離散したデータを畳み込むとどのようになるのでしょうか? 実はこちらの方が簡単に理解できます。
今度は図2を見てください。ここでは頭に〇が付いている②のパルス群と×が付いている①のパルス群とを畳み込んでみます。①は入力されたデジタル信号、②はIR(インパルスレスポンス)と思っていただいても結構です。図は(ア)~(カ)にかけて1サンプルずつ時刻が進んでいき、各図の下半分が畳み込まれた結果です。そして先程と同じように2つのパルス列が重なっている部分でY軸上に並んでいるパルス同士で大きさを掛け算しそれらを合計(重ね足し合わせ計算)します。
具体的に説明しますと、まず同図(イ)を見てください。この時2つのパルスが重なっていますね。そしてこれらを掛け算すると、それぞれ1と3ですから答えは3となります。つまり畳み込み結果は3の値のパルスが出力されます。もうひとつ次のステップ(ウ)になると重なり合っている部分が2つになりますが、最初が2×3=6、次が1×1=1で、この重なっている部分の合計7が畳み込みの結果として出力されます。更に進んで(エ)も同じように計算すると3+2で5が出力されます。このようにして2つのパルス群が畳み込まれると同図(カ)のような結果となります。これから分かるように畳み込みとは重なり合っているパルス同士をそれぞれ掛け算しそれらを合計するだけです。そう考えると畳み込みに少し親しみが湧いてきましたか?
再記すると、入力される①は入力音声信号で、②は目的の周波数特性から得られたIRで各タップの係数として設定され、この入力信号がFIR-EQ/フィルターを通った結果の出力信号が同図の(カ)ということですね。これが畳み込みの計算原理で、FIRフィルターではこのような演算が延々と行なわれているのです。
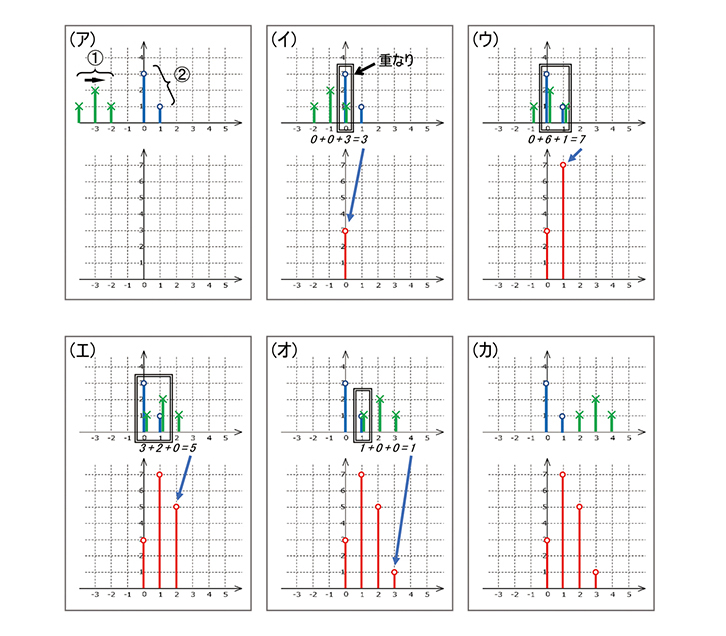
図2 パルスデータ(離散データ)の畳み込み
①が1サンプル時間ずつ右に移動して②と畳み込まれていく様子。下半分が畳み込まれた結果。詳細は本文参照
畳み込みについて何となくでもお分かり頂けましたでしょうか? これらが分かればFIRへの理解も大きく進むことと思います。これでFIRはカンペキ!?
以上で畳み込みに関するお話は終わり、ここからはFIRに関連するお話を少し。
デジタルリバーブ
歴史
冒頭で述べた“音響に従事している方なら使ったことのある畳み込みを応用した機器”とは、デジタルリバーブのことです。しかも最初にこの計算理論を応用した音響機器でもあります。
デジタルリバーブには大きく分けて2種類あります。ひとつ目は畳み込みではなくディレイを多数発生させてその間隔や量や大きさを制御する方式。1962年にM.R.Schroeder氏がAESジャーナルに掲載した概念が基本となっていますが、コムフィルターやオールパスフィルターと呼ばれるデジタル遅延回路を多数組み合わせたものでした。
この概念が実用になった最初の機器は1976年にプレートリバーブで有名なドイツの「EMT」社から発売された「EMT250」(初期モデルはEMT144)で、当時はベンツより高いリバーブと呼ばれていました。何しろ為替レートが1$=300円で国産小型車が80万円で買えた時代に$20,000していましたからね! その後、アメリカの「Lexicon」社から約半額になった「224」という名機が発売され、後の「480」と共に一世を風靡しました。自然なリバーブというよりもエフェクト的なリバーブ(例えばゲートリバーブ等)のような変わり技ができたことから当時の有名ミュージシャンのアルバムではほぼ全員が使っていたと言っても過言ではありませんし、私も大変お世話になりました。これらが放つ独特のサウンドは現在でもプラグインという形で残っていますので、ご存知の方も多いと思います。序でのお話をしますと、現在このプラグインは当時の製品価格の1/100で購入できます! あぁ時代の移り変わりを感じずには…。
話を戻して、この辺りまでのデジタルリバーブは次にお話するリバーブと区別して、アルゴリズムリバーブやシュレーダーリバーブと呼ばれます。
そして2つ目が1990年後半に登場する畳み込みを使ったデジタルリバーブで、コンボリューションリバーブやサンプリングリバーブと呼ばれるものです。この実用機は1999年に「ソニー」から「DRE-S777」、2001年には「ヤマハ」から「SREV1」と立て続けに発売されましたが、実用機としては世界に先駆けた日本発の音響機器でした!
コンボリューションリバーブ
ここまでお話してきた畳み込みは、FIR-EQ/フィルターにおける畳み込みで、直線畳み込みと呼ばれるものです(直線畳み込み以外に巡回畳み込みというものがありますが、今回は省略します)。これに用いられるIRは目的の周波数特性からフーリエ変換して求めたものを使用してきましたが本シリーズの冒頭(2019年12月号)で最も身近なIRはホールで手を叩いた時の「響き」だと申し上げたのを覚えておられますか? この「響き」は時間と共に各種の要素が変化するものですよね。ですから、その変化の状態を記録しておき、ある音にそれと同じ変化を加えることで同じような響きを持つ音を作ることができます。その演算にこの畳み込みを使います。つまりFIRフィルターのタップの各係数にこの響きデータ(=IR)を使用して入力信号を畳み込むのです。
もう少し簡単に言うと、手を叩いた「パン」という音(1サンプルのインパルス信号)にその部屋の響き(IR)を掛け算すると「パ~~~ン」という音になります。これは1サンプルだけの出力ですが、ここで、入力された信号がこの1サンプルのインパルスが連続したものだと考えると、
1サンプル目のパルス×響きのIR=1サンプル目に響きが加わった音
2サンプル目のパルス×響きのIR=2サンプル目に響きが加わった音
3サンプル目のパルス×響きのIR=3サンプル目に響きが加わった音
:
:
nサンプル目のパルス×響きのIR=nサンプル目に響きが加わった音
となりますが、これらの出力を順に1サンプル時間ずつズラして重ねてやれば入力信号に響き(リバーブ)が掛かった音が出力されることになりませんか? これがコンボリューションリバーブの動作で、実はこれが畳み込みというもの自体でもあるのです。
なあ~~んだ!でしょ!
が、しかしここで少々問題があります。FIR-EQ/フィルターで使用するIRは多くても1万数千タップです。ところがリバーブの場合、fsが48kHzで残響時間が1秒間ですとそのタップ数は48,000、3秒間ですと144,000タップとなります。これに入力信号のパルス数はfsが48kHzの場合1秒間に48,000個ありますから、演算はこれらを掛け合わせた回数が必要となります。もしfs96kHzで5秒間ならばこれの10倍です。デジタルリバーブはリアルタイムで使いますが、これだけの演算をリアルタイムで行なうことはいかに速いDSPやCPUでも現状では少々難しいのです。
そこで考えられたのが同じ畳み込みでもFIR以外のアプローチ方法です。これまでお話してきたようにFIRは時間領域での畳み込みでした。ここで思い出して頂きたいのですが、連載第1回目で「ひとつの伝達関数を時間領域で見るとインパルス応答になり周波数領域で見るとEQカーブ(周波数特性)になる。また「時間領域」から「周波数領域」に変換する方法をフーリエ変換(FFT)という」とご説明しました。FIR以外の方法とはこのFFTを使います(FFTを補足すると、離散化したデータをフーリエ変換することをDFT[Discrete Fourier Transform]と言いますが、この変換を高速で処理するPCでのアルゴリズムの名前をFFT[Fast Fourier Transform]と言います)。
入力信号もIRも共にFFTして周波数領域のデータに変換します(図3)。詳しい理論は省力しますが、畳み込み積分は周波数領域に変換すると単純な掛け算として計算できます。ここが重要! ただの掛け算なら非常に高速の計算が可能です。そしてその結果を逆フーリエ変換(IFFT)して元の時間領域のデータに戻してやります。そうすることで時間と共に変化する「音データ」になります。本当はこれにもう少し複雑な処理(先ほどの巡回畳み込み等)が加わるのですが、現在のコンボリューションリバーブでは基本的にこの方法が採用されています。
ここで「だったら何故計算が大変な直線畳み込みをせずにすべてFFTで行なえば良いのに」と思われた読者の方もおられると思います。でもこの方法には少々問題があるのです。問題とは、FFTを行なうためにはまず処理するデータを切り出さないといけないのですが、その時に窓関数というものを使います。しかしこの時にデータの正確性が損なわれてしまうのです。このデータの切り取りを行なうとサイドローブと呼ばれる雑音が発生してしまいます。窓関数はこのサイドローブ(=雑音レベル)を軽減するための処理をしているのですが、このサイドローブは元信号にはないもの(=雑音)で、切り取ることで大なり小なりそれが発生してしまうのです。正確性が損なわれるとはこのサイドローブが発生することで、元のデータに余分なものが加わってしまうのです。
参考までに、このサイドローブにはこれを軽減しようとすると反対に周波数分解能が悪くなるという二律背反の関係があり、どの窓を利用するかも悩みどころです。もうひとつ参考までに、この二律背反の関係を私達がよく聞く名前の窓関数で見てみると、図4のようになります。チューニングソフトのSmaartを使っていると、皆さん必ず悩むところですよね! ちなみに私は相対レベルよりも周波数を正確に知りたいので周波数分解能の高いハミング(hamming)を使っています。
今回は2つの全く原理の異なるデジタルリバーブのお話をしましたが、現在ではどちらも第一線で使用されており、シュレーダー方式はエフェクト的な要素が強くコンボリューション方式は自然な響きを求める要素が強いことから、それぞれの目的に応じた使い分けが行なわれています。
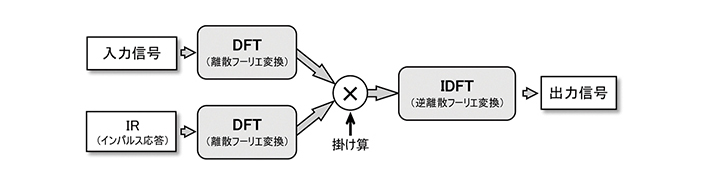
図3 DFTによるコンボリューションリバーブ
インパルス応答(時間波形)とEQカーブ(周波数波形)は、伝達特性を「時間領域」でみるか、「周波数領域」でみるかだけの違いなので、時間領域で計算量の多い「畳み込み演算」をやるよりも、周波数領域で「掛け算」で済ませる方がプロセッサーの負荷が少なくなる
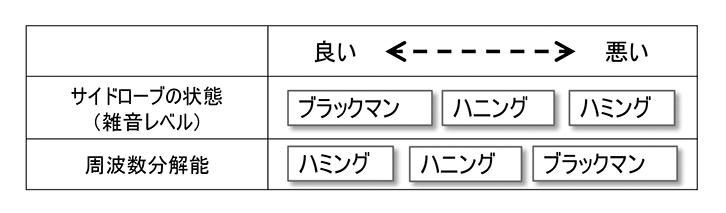
図4 各窓関数の特徴代表的な3つの窓関数の比較
サイドローブ(雑音)の状態と周波。数分解能は二律背反の関係になる
畳み込みの応用
次に、この技術がFIR-EQ/フィルター以外にどのようなものに応用されているかも見てみましょう。まず身近に思い当たるものが可聴化シミュレーション装置です。これは建物の形状を入力し各壁面の吸音率データを入力してスピーカーをプロットすると、指定した場所で実際にどのように聴こえるかを疑似体験することができるものですね。指定した場所での直接音や反射音の状態はスピーカーの指向性や周波数特性からどの壁面にどの程度反射して到達するかが計算できますので、音声や音楽をこの直接音を含む反射音データ(=IRデータ)と畳み込むことでその場所の聴こえ方がシミュレーションできます。また、同時に直接音と反射音の状態がわかりますのでSTI(明瞭度指標)も計算できます。よく考えると、これは先程のコンボリューションリバーブと同じことをしているのですね。
音以外では、映像でスピード感を出すためにブレた画面を作るモーションブラーと呼ばれるエフェクトがありますが、その効果を作る時にも使用されています。このモーションブラーは言い換えると映像でのコンボリューションリバーブ処理です。また、今流行のAIの分野でも応用されており、膨大な数の画像を深層学習するためのニューラルネットワーク(CNN)というものがありますが、その根幹技術にもこの畳み込みが使われています(CNNの最初のCはConvolutionです)。また、天気予報に使う気象データの解析等にもこのCNNが応用されています。私達とは別の世界でもこの畳み込みは大活躍しているようですね。
まとめ
今回の特集では全3回に渡って多くの事柄をお伝えしてきましたが、それらの要点を簡単にまとめてみました。
1. インパルスとは、すべての周波数を同位相・同レベルで持ったもの
2. それをあるブラックボックスに入れて出てきたものがインパルス応答
3. インパルス応答はそのブラックボックスの中身を表している
4. インパルス応答(時間情報)をフーリエ変換(周波数情報に変換)すると周波数特性となる
5. その時に各周波数がどのぐらい遅れて到達しているかを見ると位相特性となる
6. 周波数と位相の遅れが比例していれば群遅延は一定
7. インパルス応答の長さは周波数と比例する (長い=周波数が低い)
8. f0(周波数解像度)=fs(サンプリング周波数)÷タップ数
9. Dt(遅延時間)=(タップ数/2)÷fs(直線位相の場合)
10. 各タップの係数はインパルス応答より求める
11. FIRは入力信号とインパルス応答を畳み込むための演算器
12. インパルス応答が分かればあらゆるフィルターが作成可能
13. 複雑な波形も逆フーリエ変換するとそのインパルス応答が得られる
14. 従ってFIRはいかなる形状のフィルターも作成可能
15. 当然従来のようなEQ特性を作ることも可能
16. 畳み込みは2つの関数の合成方法のひとつ
17. 畳み込みを使った最初の音響機器はコンボリューションリバーブ
18. 畳み込みは音響以外でも多くのものに利用されている
近い将来
今回お話してきた中で、FIRが持つライブサウンド的に見た場合の最大のウィークポイントは、直線位相を求める場合に発生する「遅延」でした。扱う周波数が低ければ低いほど多くの遅延を発生します。しかしこの問題は、次のような方法で解決することが可能になるかもしれません。いや、なるでしょう!
それは全周波数を数帯域に分けて処理する方法です。実際にこの概念はマルチレート処理と呼ばれており、かなり以前から実証実験が行なわれています。ちなみに、2000年頃に設計されたリニアフェーズクロスオーバーを謳った「Lake」社の「Contour」や最近話題になった8192タップ(fs96kHz)でも13msecのレイテンシー(※2)を謳った「CODA AUDIO」社のプロセッサーには既に一部このやり方が使われています。
この方法とは、例えば低い周波数域で高い解像度を得ようとするとき、ここが一番の問題点なのですが、低いfs(サンプリング周波数)でサンプリングしてやると少ないタップ数でも高い解像度(=低い周波数を扱える)が得られます(前項「まとめ」の8)。しかしこのままではfsが低いので高い周波数が扱えません。そこで高い周波数域ではそれなりに低い(荒い)解像度でも実用になりますので、帯域分割して帯域毎に最適なfsでサンプリングしてやれば少ないタップ数(=短いレンテンシー)でも実用になります。そして、これらのデータを最終的にひとつにまとめてやると低い周波数が扱えるにもかかわらず遅延の短い直線位相FIRが実現できることになります。
この説明でSmaartの伝達関数を表示する時に使われるFPPO(Fixed-Point per Octave)を連想された方もおられたと思いますが、正解です。それもマルチレート処理のひとつです。
実際の方法としては、図5のように最高帯域以外はダウンコンバートして目的の信号処理(直線位相FIR等)し、その後アップコンバートして最高帯域のデータと時間軸を揃えて全体域データとして合成します(前述のLakeやCODA AUDIOのプロセッサーは最終部分で合成せずにそのままパワーアンプに入力しクロスオーバーとして使用されています)。
この図は3分割処理ですが、もっと多くの帯域に分割し、帯域とタップ数を適切に組み合わせることでより短い遅延の直線位相FIRを実現することができると思いませんか。
もうひとつの問題は、目的のEQカーブを作るという作業のうちで音場補正をしようとすると、現状の伝送特性を取得してそれを元に逆特性カーブを作る作業が必要です(位相補正も同じ)。しかし、どのFIR機器を見てもその手順は煩雑で、しかも一度取り込んだ後で演算するという手順のためにリアルタイム性がありません。しかし伝送特性を取込みながら逆特性を演算することができればチューニングの作業性は格段に向上します。FIRフィルターでライブ中に今の状態をリアルタイムで補正することが可能になるかもしれません。
実は、この技術のひとつを“Real Time Deconvolution”という名前でEASEで有名な「AMFG」社が特許を持っており、チューニングソフトのSysTuneがそれに近いアルゴリズムで計算しています。これには高速演算するための特殊なプログラミングが使用されているのですが、OSレベルまで踏み込める高度なプラグラミング技術が必要(AMFGによる)とのことです。しかしこの概念に到達できそうなことがすでに行なわれているということですね!
色々調べてみると、これらのことは近い将来に充分に実現可能な技術なのだと分かりました。ということで、私も皆さんと共に首を長~~くして待ちたいと思います!
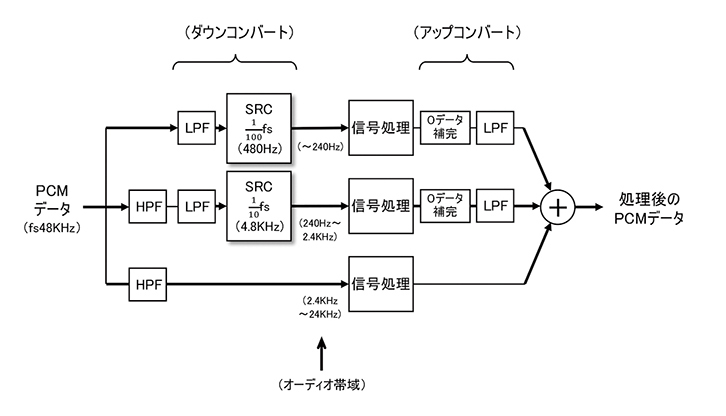
図5 帯域分割信号処理の概念
処理する周波数の帯域を分けて遅延の少ないFIRを実現する方法(本文参照)
※2:本特集ではFIR処理による遅れを「遅延」、システム全体としての遅れを「レイテンシー」として区別しています。
最後に
本シリーズは最近話題になっている「FIR」についてお送りしました。その中では数学や物理のお話をしなければならないところが多数あり、できる限り平易に説明しようとトライしてみたのですが、説明が不充分で理解に苦しまれた部分があったかもしれません。ただ、何となくでもお分かり頂けたのであれば幸いです。
しかし読者の方の中には更にもっと詳しく知りたい、そこは何故そうなるの?と思われた方も多くおられたのではないかと思います。実はそのような方々のために最適なセミナーがありますのでご紹介します。それは、
今回のような雑誌では限界があり詳しく説明するのがなかなか難しい内容を平易なテキストとプレゼンテーションツールで非常に分かり易く解説して頂けます。主宰されているのは、元「TOA」のエンジニアであのウィーン国立歌劇場にも導入された世界初の業務用フルデジタルコンソール「ix-9000」の開発責任者を務めた栗山譲二氏です。
このセミナーは今回のようなデジタル信号処理だけではなく、音響に関わる多種多様な内容の講座があり、それぞれ非常にエレガントに説明して頂けます。また、昨今の状況に合わせてオンラインセミナーも選択できます(高いセキュリティ機能を持つウェビナーシステムを使用しているとのこと)。興味のある方は是非上記のURLにアクセスしてみてください。必ずためになる情報が得られると思います。
以上で今回の特別企画を終了いたしますが、「FIR」をより身近に感じて頂けましたでしょうか?
どのような機器でもその動作原理を理解しながら使うとより正確に且つより深く扱うことができるようになるものです。その時には、またひとつ成長した自分が見えるかも分かりませんね!
最後に、この特集にご協力頂いたJ.TESORI様に深く謝辞申し上げます。
面白い情報が得られると思いますので是非一度 J.TESORIホームページ ![]() にアクセスを!
にアクセスを!
※文中のSmaartは「Rational Acoustics」社、EASEおよびSystuneは「AMFG」社の登録商標です。
筆者紹介 --------------------------
三村美照(みむら・よしてる)
音響システム設計コンサルタント。1978年「スタジオサウンドクリエーション」に入社、レコーディング・エンジニアとして経験を積む。その後、業務用音響機器の設計業務を経て、1989年から「アキト」において本格的に音響システム設計に従事、現在「M&Hラボラトリー」代表取締役を務める。仕事においては「ベストを考えない、ベストとは逆に「終わり」を意味する。私たちの仕事に終わりはない」、「常により良いものを、よりシンプルに」をポリシーに「設備の音」を築き続けている。豊田スタジアム、長居陸上競技場、新広島球場、サンケイホール、大阪フェスティバルホール、国立京都国際会議場等をはじめ実績例は100件以上と多岐多数
Copyright © Yamaha Sound Systems Inc. All Rights Reserved.