短期集中連載 超解説FIR! 第2回
短期集中連載
超解説FIR!
第2回
三村美照(M&Hラボラトリー)/兼子 紳一郎(ヤマハサウンドシステム) イラスト:あや

前号に引き続き「超解説FIR!」の第2回目をお送りします。1回目の内容は下記目次をご覧ください。また、より理解を深めるために記事もぜひ御一読ください。なお、この連載は毎号皆さんの意見を受けながら加筆していますので、目次はその都度変更されることがあります。ご了承ください。

●
第1回目の最後でインパルス応答の長さについてのお話をしました。そこには周波数解像度というものがあり、それはTap(タップ)数とfs(サンプリング周波数)に関連することが分かりました。
復習すると、FIRの場合、
周波数解像度f₀=サンプリング周波数fs÷Tap数 ------ ①
という関係でしたね。
この周波数解像度というものは、低い周波数を操作しようと思えばこの値を小さくする必要があります。つまり、周波数解像度が50Hzならば操作可能な周波数は50Hzから始まって100Hz、150Hz、200Hz……と50Hz飛びになり、75Hzや125Hzを操作しようと思ってもできません。
そこでこの解像度を小さくするためには、①式からも分かるようにfsを下げるかTap数を上げるということになります。このうちfsを下げてしまうと扱える最高周波数も下がってしまうのでこれは却下(※1)。そこでTap数を上げることになります。しかしそこには大きな問題が!…というところで前回は終了していました。今回はその続きですが、そのお話を続ける前に、そもそもTap数って何?というお話しをしなければなりません。
※1:実は敢えてこれを行なう方法が最新のテクノロジーのひとつになっているのですが、詳細は3回目でご説明します。
「FIR」って何?(2)
Tap数の「Tap」とは何か?を説明するために、まずFIRの中身を見ていきましょう。このFIRですが、Finite Impulse Responseの頭文字をとったもので「有限インパルスレスポンス」のことでした。そして「有限」があるなら「無限」も存在し、それを「無限インパルスレスポンス(IIR)」と呼ぶというお話もしました。
ではこの「FIR」と「IIR」ですが、違いはそれらがどのように信号を処理しているのかが分かると理解しやすくなります。先ずはIIRから。
・IIRの信号処理
図1-Aを見てください。この図はIIRの信号処理の流れを示した演算ブロック図です。この中には幾つかシンボルや記号がありますので、まずそれについて説明します。
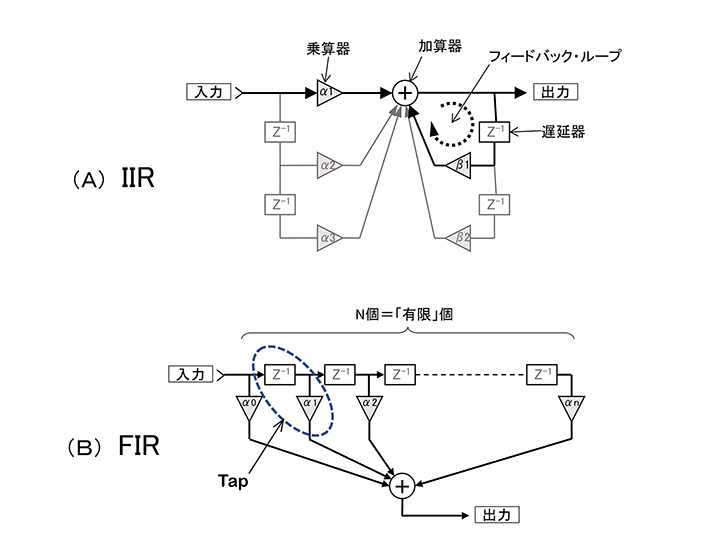
図1 IIRとFIRの違い/演算ブロック図の比較
・遅延器
四角形の中に「Z-¹」と書かれたものが遅延器です。遅延器とは言葉の通り1サンプルサイクルだけ処理を遅らせます。IIRでもFIRでも入力されるサンプルは連続的に送られてきますから、ひとつ処理を遅らせることで順に並んでいるサンプルのひとつ前のサンプルが処理できます。この「ひとつ前のサンプル」とは、並んでやってくるサンプルの順番を示していますので実際には次の音のことになります。
・乗算器
三角形をしたものが乗算器です。乗算とは掛け算のことですね。では掛け算するとは具体的にどのようなことを行なっているのでしょうか。
ここでは入力されたサンプルの中身(量子化された二進数のデータ)に対してある「係数」を掛けています。この掛け算自体は単純に数学的な二進数の掛け算ですが、FIRとIIRではこの係数の求め方が違います。
まずIIRの場合ですが、これは求めるフィルターカーブを信号処理理論に基づいてアナログフィルターからデジタルフィルターへの変換式(S-Z変換という)で導かれます。通常のフィルター(EQ)で必要なカーブは割と単純なカーブですから求める係数も比較的簡単に求められます。
一方、FIRの係数はインパルス応答波形から求めます。前号の(図7)にインパルス波形とフィルター特性の関連を示しましたが、このインパルス応答波形から係数を導き出し、各乗算器に当て嵌めることで目的のフィルターカーブを得ることができます。
これらが分かったところで再度、図1-Aを見てください。まず入力された信号は最初の乗算器を通って出力されます。乗算器には遅延はありませんから入力された信号はすぐに出力されます。更によく見ると、3つのフィードフォーワードと2つのフィードバックループがあるのが分かります。この内のフィードバックループでは、信号がグルグルと何時までも回り続けながら信号を出力し続けることができます。つまりインパルスの応答を無限に出し続けることが可能で、これが“無限”インパルス応答「IIR」と呼ばれる理由です。もちろん、出力が減衰せずに無限に続いてしまうと発振状態になり現実的には使えません。ただ係数によってはその可能性があると言えることから、安定性という面ではアナログと同様に完全に安定的な処理方法とは言えません。
一方、フィードバックを起こして長いインパルス応答を出力できるということは、長いインパルス応答=低い周波数ということでしたので、発振状態にならないように気をつけさえすれば充分に低い音まで処理できるということになります。
IIRは、同図のような簡単な構成ですが、各係数を適切に変化させることによりアナログで可能なすべてのフィルター(EQ)カーブを作り出すことができます。また、この図の構成でEQの1ポイントとなりますので、8ポイントEQの場合はこれを8組シリーズに接続して処理が行なわれます。
よくマルチポイントEQで、あるポイントだけPEQやHPF、更にはShelfタイプのEQ等に変更できるものがありますが、この仕組みが分かると「なるほど!」と思いますでしょ!
FIRの信号処理
やっとFIRのお話になりますが、ここからは特に注釈がない限り直線位相のFIRのについてです。FIRにはそれ以外にも最小位相等がありますが、このお話は後ほど。
・タップとは
図1-Bを見てください。先程の図と異なり、「Z-1」の遅延器とその下にある三角形の乗算器が直列に幾つも並んでいますが、この遅延器と乗算器の組み合わせを「タップ」と呼んでいます。
このタップは幾つか並んでいますね。つまり有限個並んでいます。そしてこれらのタップを通過することで一連の処理が一段落しますが、この時出力されるパルスの数はタップ数に関連する決まった数、つまり有限の数しか出力されません。これがFIRの「F(Finite=有限)」の意味です。無限の出力が可能なIIRとはここが違います。FIRではこのような処理をしていますのでIIRのように発振することはなく安定していますが、タップが多ければその分だけ処理量が多くなり時間が掛かかります。低い周波数=長いインパルス応答=多くのTap数=長い遅延ということになりますので、これがライブサウンドでは使いにくい原因となっているのですね。
では具体的にどの位遅延時間が発生するのでしょうか。
・FIRの遅延時間(1)
FIRの遅延時間は2つの方法で導き出されます。まずはインパルス応答波形から。
図2は前号でも出てきた直線位相の場合のインパルス応答です。この図のf₀は周波数解像度の周波数(=最低周波数)で、fsの半分までの信号でf₀の倍数の周波数で群遅延が一定になる(位相の変化が無い)ように重なっていることを示しているのですが、ちょうどf₀の波長の半分のところに合成波形のピークができます。直線位相のFIRではこのピークの位置が遅延時間となります。例えば、最低周波数が50Hzの場合、この一波長は時間でいうと20msecですから、その半分の10msecが遅延時間ということになります。
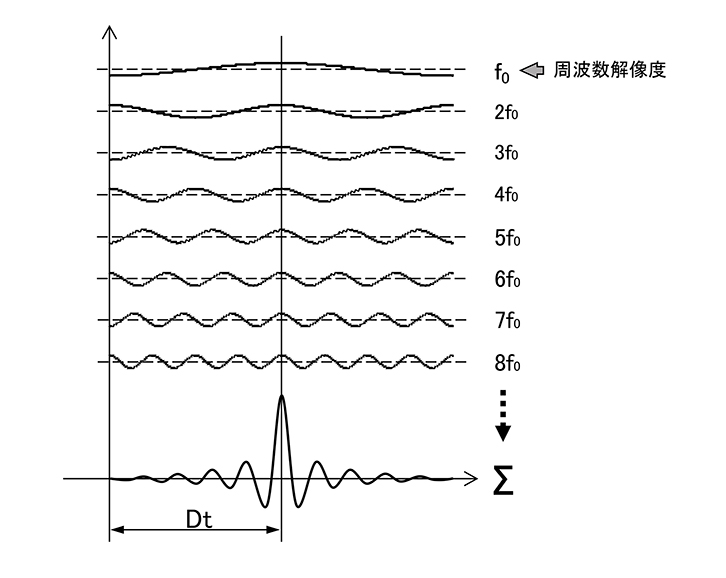
図2 直線位相のインパルス応答波形
f₀からfsによる最高周波数までの倍音がすべて群遅延一定で合わさるとf₀の中心にピークができる。その時間Dtが遅延時間。何故?これは本文参照
・FIRの遅延時間(2)
2番目はTap数から導き出せます。Tap数の半分の数に対して、そこに入力される1サンプルに必要な時間を掛ければ出てきます。つまり、
遅延時間=(Tap数/2)×1サンプル時間
ここで、1サンプル時間とは各サンプルが出力される間隔でサンプリング周波数fsの逆数ですから、この式は
遅延時間Dt=(Tap数/2)÷ fs ---------- ②
と書くことができます。これを1024Tapでfs48kHzの場合で計算すると(1024/2)÷48000≒10msecとなります。
ところで、「なぜTap数の“半分”なの?」という疑問が出てきませんか?
・なぜTap数の半分?
ここでまず、インパルス応答は拡大すると図3のようにTap数に対応する数のパルスで構成されています。実は連続したものではなく、このように離散した(ひとつひとつ分かれた)ものなのですね。今回、直線位相のピーキングEQをブーストした時のインパルス応答を用意し、このFIRから出力されるデータがTapごとにどのように変化していくかを切り取ってみました。
図4-ア~カをご覧ください。
(ア)先ず(図4-ア)ですが、最初のサンプルは遅延器無しで乗算器を通過しただけで出力されます(図1-B参照)。いま仮にこれに使用したパルスの位置を時間的な0点(現在時刻)とします。ここが重要です。
(イ)次に最初のパルスのひとつ+側のパルス①が用いられて演算が行なわれ振幅特性が変化し始めます。それと同時に位相も変化します。
(ウ)そしてその次のサンプルが入力されますが、これは先程と対称位置の-(マイナス)側のパルス②が用いられています。そして、この時の位相特性を見てください。フラットになっています!
(エ)そして次の③が入ると再び位相が乱れますが、
(オ)その次の対称位置のパルス④により位相がフラットに戻っています。
(カ)これを繰り返し最終的に(図4-カ)のような波形になります。
このように左右対称にパルスを処理していくことで位相はフラットになります。これは+側のパルスで変化した位相を-側のパルスで元に戻しているという感じでしょうか。
しかしよく考えると、-側というのはサンプル信号がフィルターに入力されるよりも“前”にそのサンプル信号に乗算をしなければならないのです。当然このようなことはできません。そこでインパルス応答全体を右側にシフトするすると-側がなくなるので実現可能な処理となります。この「インパルス応答を右側にシフトする」とはインパルス応答を遅らせることですので、そのシフトした分=全Tap数の半分が遅延時間ということになるのですね。お分かりいただけたでしょうか?
このことからも分かるように、直線位相ではそのインパルス応答が必ず対称形であることがポイントになります。
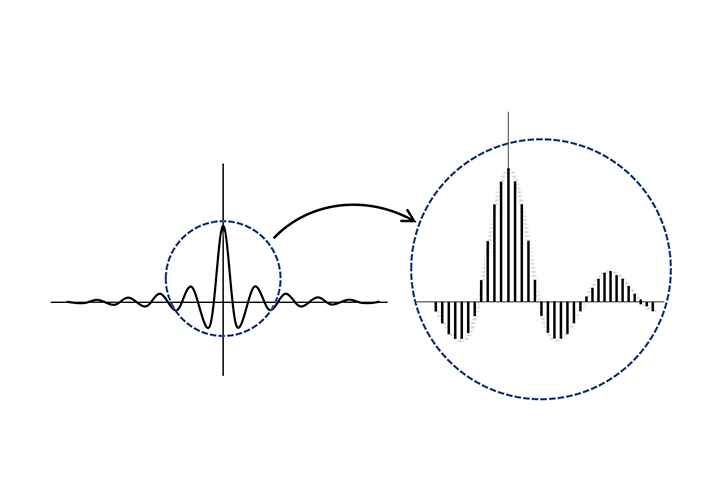
図3 インパルス応答図を拡大すると…Tap数と同じ数のインパルスで構成されている
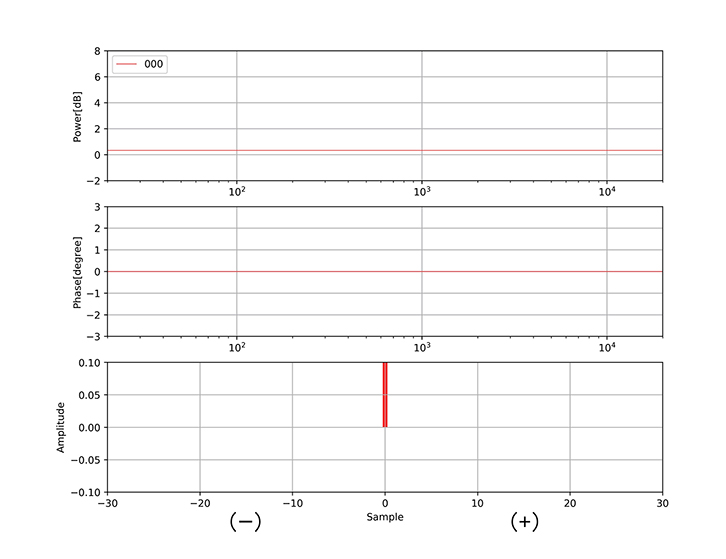
図4-ア 上段が振幅特性、中段が位相特性、下段がインパルス応答のステップ
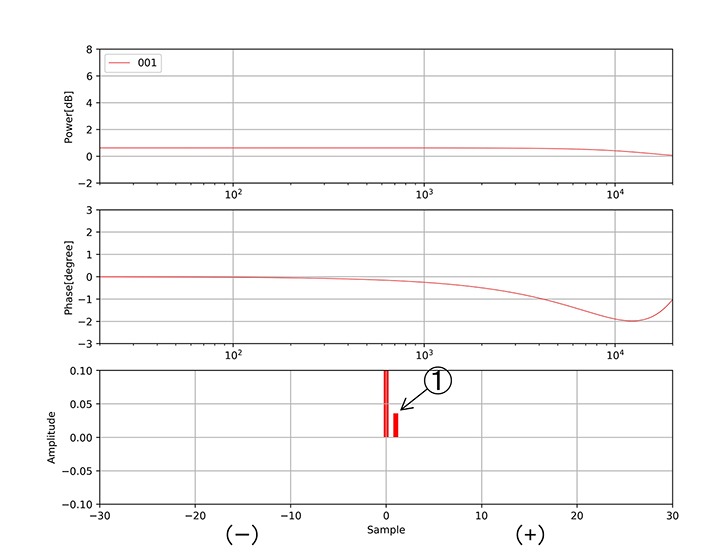
図4-イ ①のタップによる変化の様子。振幅特性と位相特性は共に変化
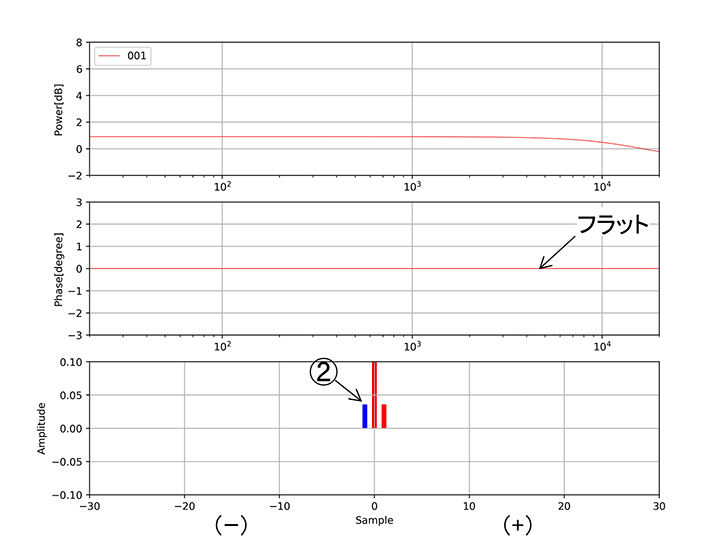
図4-ウ ②のタップは-(マイナス)側で①の対称位置。この時、位相特性はフラットになっている!
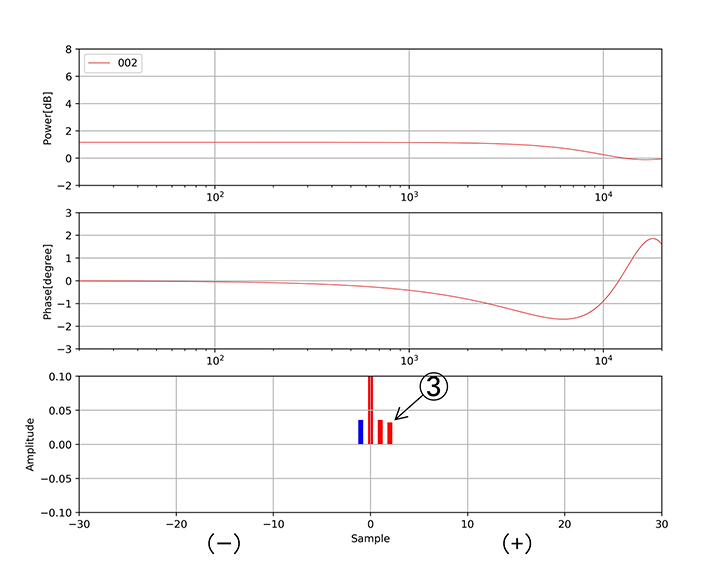
図4-エ タップ③で位相特性が再び変化
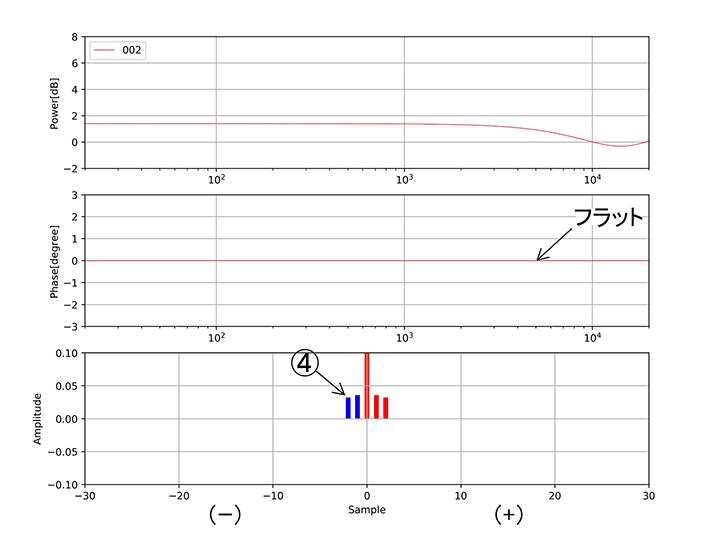
図4-オ タップ④は③の対称位置(マイナス側)。
この時の位相特性は再びフラットになっている
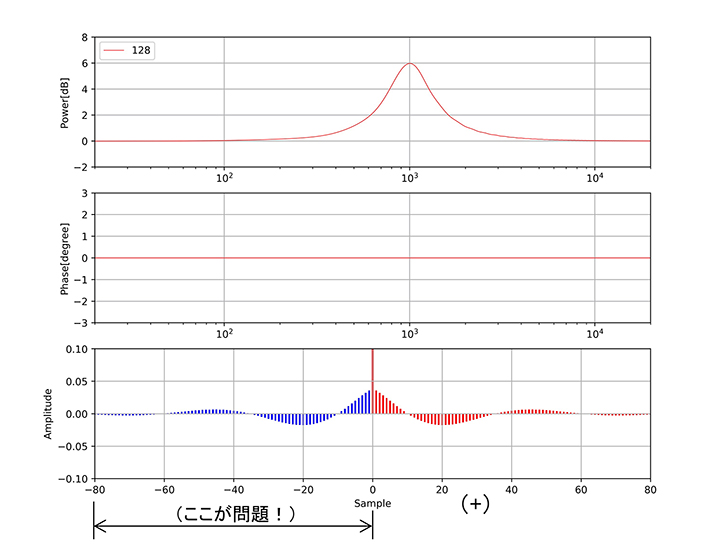
図4-カ 最終形は直線位相のピーキングEQ。
インパルス応答は対称形になっている。この時、0サンプルよりマイナス側のパルスが問題。これらは今よりも前にタップがあることになり、あり得ない!そこでどうする? 詳しくは本文参照
・直線位相FIRと最小位相FIR
ここまでは位相の変化しない直線位相のFIRのお話をしてきましたが、懸命な方は気付いておられるかもしれませんが、「FIRは位相が変化しない」という言い方は正しくはありませんね。「変化しないようにも作れる」と表すのが正しい表現です。変化しないものは直線位相FIRですが、最小位相FIRと呼ばれるIIRと同じような位相の変化を伴うものもあります。この2つの違いはインパルス応答で見ると、図5のようになります。
これから分かるように最小位相のインパルス応答は対称形でなくピークが0の所に来ています。このことは先程のシフトをする必要が無いということで、直線位相FIRよりも短い遅延時間で出力が可能となります。最小位相FIRにはこのようなメリットがあるのですね。
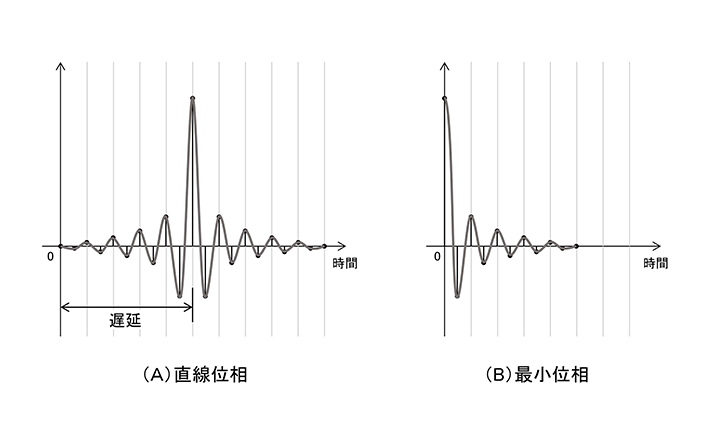
図5 直線位相と最小位相のインパルス応答。
ピーク位置の違いが遅延時間の違い。何故かは本文参照
アナログでは実現不可能なフィルターが作れる!
ここで最初のお話に戻りますが、FIRは複雑な計算をしなければならないし直線位相の場合は大きな遅延も発生します。しかし何故それでもFIRを使うようになって来たのでしょうか?
FIRはTapにある乗算器の係数を操作することで目的のフィルター特性を作り出し、この係数自体はそのフィルターのインパルス応答そのものです。この時の動作は、サンプルデータが入力されると次々と各乗算器で係数(インパルス応答)と掛け合わされて(正確には「重ね足し合わされる」と言います)データが吐き出されます。詳しくは次回で説明しますが、この一連の動作を畳み込みと言います。入力信号(サンプルデータ)とインパルス応答波形の2つを畳み込んで新たなデータを作り出しています。つまりFIRの実態は「畳み込みをするための演算器」なのです。
また、乗算器の各係数はインパルス応答そのものだと書きましたが、このことはインパルス応答さえ分かればどのようなフィルターでも作れると言い換えることができます。つまり、前号の「図7 インパルス応答と周波数特性」にあるインパルス応答を係数として各乗算器に入力すると、それに対応したフィルターカーブを作ることが可能ということです。
また前述の通り、FIRは位相が変化しないのではなく、変化しないようにも作れるということですから、そのインパルス応答さえ分かれば、IIRのように最小位相として位相が変化するものも作れ、短い遅延時間のメリットが活かせます。また、「LAKE」のような非対称カーブを持つEQのMesa-EQも可能です。それのみならず、ここからが重要なのですが、適当な周波数カーブを描いてそれを逆フーリエ変換(※2)すれば、カーブのインパルス応答が得られます。そして、そのインパルス応答を乗算器の係数に入れてやることでその適当に描いたカーブのフィルターを作ることができるのです。どんなに複雑なカーブもです!
FIRフィルターを使って音響チューニングをする時には、測定した周波数特性の逆特性をソフトウェアで作って補正しますが、その一連の動作は正にこれをやっているのです。あの複雑な周波数特性の逆特性フィルターをいとも簡単に作ってしまえるのは、そのような理由からだったのですね。以前、FIR-EQには周波数・Q・ゲイン・ポイント数等という概念がなく全体をひとつの関数として扱うと書きましたが、これがその理由です。
更に応用として、あるスピーカーの特性(音)を別のスピーカーに近付けたいとします。そこで基準になるスピーカーの周波数特性を求め、それを基準に対象のスピーカー特性との差分を求めてやれば簡単に同じ特性となるような補正ができます。これを従来のEQを使ってアナログ的に行なおうと思えば非常に大変な作業になることは皆さんなら容易に想像できますよね。
更に更に、前述のようにして作ったカーブに加えて従来のIIRのように周波数・Q・ゲインを加味したカーブを追加することもできます。つまり、それらを含めてひとつのカーブ(関数)として扱えば良いのですからね。
「FIRはアナログで実現不可能なフィルターが作れる!」という意味がお分かりいただけたでしょうか。そして正にこのことが、今FIRが注目されている理由なのです。
ところで、このように非常に高い能力を持つFIRフィルターですが、それを用いたチューニング作業を行なう場合の注意点をひとつ。
これは従来のチューニングでも言えることなのですが、重要となるのが測定した周波数特性のデータで、一般的な方法で取得したデータはマイクを少し移動するだけで特に高音域等は大きく変化する時があるのは皆さんもご存知の通りです。このような状況で、あまり厳密にひとつのデータだけを基に操作してしまうと、そのマイク位置だけの特性を操作してしまうような無駄な補正をしてしまいがちです。前述のようにFIRはどのようなカーブも作れてしまうのです。そこでそのデータをある程度丸める作業であるスムージングや操作する周波数範囲を限定する必要が出てきます。どの範囲を選びどの程度スムージングするかは非常に重要で、オートマチックで万能に思えるFIRですが、やはり操作する人の“勘所“が必要になる部分は残るということですね。最後は出音を聞いての判断ですからね。
また、FIRでフィルターカーブを作るとき、位相に関してはIIRのように最小位相として変化するものと直線位相のように変化しないものの、どちらも作ることができるのはお分かりただいたと思いますが、この二つの違いは遅延時間の違いです。
つまり、遅延を短くして振幅特性の補正を優先したければ最小位相FIRでの処理になりますし、遅延をある程度許容し位相が変化しないことを重視したければ直線位相FIRでの処理になります。この部分も「何をしたいか?」という皆さん自身の選択が重要な部分ですね。
※2:正確には離散逆フーリエ変換。フーリエ変換に関しては2019年10月号P.83をご覧ください。
最低周波数と周波数解像度が違う?
最後に面白いアイデアをご紹介します。
直線位相の場合、周波数解像度f₀、Tap数、遅延時間Dt、サンプリング周波数fsの関係を整理すると、
周波数解像度f₀=サンプリング周波数fs÷Tap数 ------ ①
遅延時間Dt=(Tap数/2)÷fs ---------- ②
でした。
ここで前号からの問題を整理すると、直線位相にしたいのだがfs96kHzで1024Tapの場合、周波数解像度(=最低周波数)は96kHz÷1024≒94Hzとなり扱える周波数は94Hz、188Hz、282Hz・・・と94Hzステップとなってしまいます。そこでTap数を10倍の10240に増やすと周波数解像度は9.4Hzとなり何とかOK。しかし今度は遅延が10240/2÷fs≒53msecとなり使えない…でした。
そこであるメーカーから周波数解像度と遅延を分けて考えた機器が登場しています。この機器ではTap数をそのままにして、図6のように強制的にピークの位置からある時間より前のデータを切り捨てています。例えばそれを5msecとすると、遅延時間は5msecとなり、直線位相になる周波数は同図の3f₀からの周波数となります。この周波数は5msecが半波長となる周波数ですので100Hzですね。ただ、厳密にはスパッと切り捨てられない(窓関数が必要)ので、直線位相となる周波数はもう少し上の周波数からになると思われます。一方Tap数は変わりませんので、周波数分解能はそのままです。この場合の100Hz以下ではその 周波数解像度のまま通常のEQのようなフィルターでの操作が可能です。
周波数分解能と遅延時間を両立させるこのアイデアはFIRに於けるひとつのソリューションかもしれません。なお、周波数解像度と遅延時間の両立に関しては直線位相のままで行なう更に面白い方法があります。それは第三章で。
…次号へつづく。
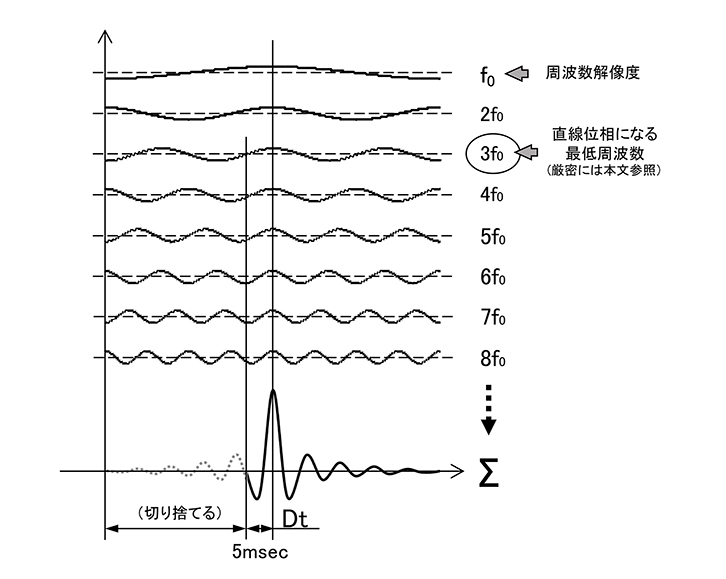
図6 直線位相になる最低周波数と周波数分解能を区別して考える。
遅延時間と最低周波数との両立方法その1
筆者紹介 --------------------------
三村美照(みむら・よしてる)
音響システム設計コンサルタント。1978年「スタジオサウンドクリエーション」に入社、レコーディング・エンジニアとして経験を積む。その後、業務用音響機器の設計業務を経て、1989年から「アキト」において本格的に音響システム設計に従事、現在「M&Hラボラトリー」代表取締役を務める。仕事においては「ベストを考えない、ベストとは逆に「終わり」を意味する。私たちの仕事に終わりはない」、「常により良いものを、よりシンプルに」をポリシーに「設備の音」を築き続けている。豊田スタジアム、長居陸上競技場、新広島球場、サンケイホール、大阪フェスティバルホール、国立京都国際会議場等をはじめ実績例は100件以上と多岐多数
追記
読者の方から、前号(2019年10月号)の「1bitは何dB?」の説明の中で誤解を与える表記があるのでは?とのご指摘を頂きましたので、補足説明します。
まず、dBは物理量の比率を対数で表したもので、比率ですから何かの基準があります。その基準値に対する大きさの比率を表した数値です。前号の中にあるように1bitは、その段階の数が2の1乗、つまり2ですから2倍の大きさの比率を表すことができます。2倍とはdBで表すと20log2=6dBとなり6dBの大きさの比率(違い)を表すことができます。これに従うと16bitは6dBが16個集まりますので6dB×16=96dBとなり、96dBの大きさの比率を表すことができます。これを音の大きさで言い換えると無音(物理的ノイズがない理想状態)から一番大きな音までの比率が96dBということです。つまりダイナミックレンジということですね。一方、このときの段階はどうなっているかというと、16bitは2の16乗ですから65536段階。このことから16bitは96dBというダイナミックレンジを65536段階で表現できるということです。
また、0(無音)を基準にすると言いましたが、現実的には0はノイズの中に埋もれてしまっていて曖昧ですし、最小bit付近の小信号は量子化するときに多くの誤差を生じます(量子化雑音)。そこで扱える最も大きな値、それをフルスケール(FS)と言いますが、それを基準にして、16bitはFS-96dBまでを65536段階で表現できるハズと書いた方が現実的かも分かりませんね。
Copyright © 2024 Yamaha Sound Systems Inc. All Rights Reserved.