短期集中連載 超解説FIR! 第1回
短期集中連載
超解説FIR!
第1回
三村美照(M&Hラボラトリー)/兼子 紳一郎(ヤマハサウンドシステム) イラスト:あや

日頃から音響に携わっておられる皆さんですが、最近よく「FIR」という言葉を耳にしませんか? しかしこれは最新の技術というわけではなく、すでに多くの機器で使用されています。では何故、最近になって私たちが耳にする頻度がここまで増してきたのでしょうか? それはライヴサウンドでもFIRが使用されるようになってきたからなのです。不思議ですね、どうして今まで使われなかったのでしょうか?…実はこの理由を考えた時こそ、FIRの特徴がよく理解できるチャンスなのです。
このFIRという言葉がEQに関連して頻繁に登場することは皆さんもご存知のとおりですが、しかし従来のEQと比べて何がどのように異なるのかを考えた時に「?」がいっぱい出てきますでしょ? その「?」を難しい数式や計算を用いずにできる限り解消しようと企画されたのがこの「超解説FIR!」です。最後まで読んでいただくと、その「?」の多くは解決されている!……ハズです。
なお、本コーナーでは非常に専門的な部分もできる限り分かりやすくご理解いただけるよう、この分野の第一線で活躍しておられる「ヤマハサウンドシステム株式会社」の兼子紳一郎氏にもご協力を賜りました。

はじめに
早速ですが、そもそも皆さんはFIRフィルターについて次のような疑問を持たれたことはありませんか?
・そもそもFIRって何?
・FIRはレイテンシーが大きいの?
・FIRは何故低い周波数を操作できない?
・レイテンシーと最低周波数には関連がありそうだが…等々
また、よく使われる単語が分からない!
・信号処理?畳み込み?インパルス応答?タップ数?
さらに、勉強していくと出てくる疑問点として、
・タップ数とサンプリング周波数と周波数解像度とレイテンシーの関係は?
・FIRではアナログで実現不可能な特性(位相だけの操作など)が作れる? 何故? どういうこと?
いかがですか? 頷いておられる方が多いのではないでしょうか。では、これらの疑問をこれから少しずつ解明していきましょう。
レイテンシーと遅延
本題に入る前に重要なことをひとつ。本文中に「レイテンシー」と「遅延」という言葉が何度も登場しますが、ここではそれらを次のように定義して使い分けたいと思います。
レイテンシー:機器内のデジタル信号の伝送経路で生じる遅れ
遅延:FIRフィルターで実現するEQ特性に依存する遅れ
デジタル信号とアナログ信号
これからの内容はデジタル信号を扱う時のお話です。アナログ信号とデジタル信号、これらは何が違うのか。それは「連続しているか?していないか?」の違いです。では「連続していない」とはどういうことでしょうか?
アナログ信号では、ある値とある値の間に無数に値が存在していますよね。一方、デジタル信号の場合はある値から次の値へはポンと飛びます。例えていうと、スロープ状の坂道に平行して階段があった場合のその2つの違いのようなもので、坂道をアナログ信号とすると階段はデジタル信号です。つまりスロープをfs(サンプリング周波数)と呼ばれるクロック信号ごとにデータを切り出すとスロープに沿った階段ができます。この作業を標本化(サンプリング)といいます。クロックとクロックの間にあるアナログ信号はデータ化されません(このように連続していない信号のことを離散系の信号と呼びます)。
量子化
クロック信号によって切り出された各信号はある大きさを持っています。その大きさを表す時に使うのがbit(※1)です。16bitや24bitというアレです。bitは0か1を表す2進数の単位で、16bitはこのbitを16個使って大きさを表します。0や1が16個並んでいる状態、これが16桁の2進数です。従って16bitで表せる段階は2の16乗=65,536段階ということになります。そして、このようにクロック信号によって切り出されたサンプルデータを2進数に変換する作業が量子化です。
※1:bitとはbinary digitから来ており、binaryは「二進数」、digitは「ケタ」の意味ですから binary digit は 「1桁の2進数」という意味になります。
1bitは何dB?
前述の計算のように(n)bitの段階の数は2の(n)乗で表わされますから、1bitは2の1乗(21)となり、21は2のことですから2倍ですね。従って1bit=20log2となり、=6dBの大きさを表すことになります。このことから、16bitは6dBが16個集まった96dB(6dB×16=96dB)の大きさを表すことができます。同様に24bitは6dB×24=144dBの大きさを表せます。これらの数字は扱えるデータの最大量を示していますから、そのbit数のダイナミックレンジということになります。
PCMデータ
前述した標本化と量子化により、できたデータがPCMデータ(正確にはリニアPCMデータ)となります。また、アナログ信号からこのデータを作ることをAD変換(ADC)といいます。16bitのPCMデータの1サンプルは0と1が16個並んだものですが、このPCMデータに各種のヘッダを付けてひと纏めにしたものをコンテナ形式(RIFF形式)にしたものが、皆さんもよくご存知の.wavの拡張子が付いたWAVファイルです。
今回お話しているデジタル信号処理とは、このPCMデータを処理することを指します。
ワードクロックとビットクロック
デジタルデータはアナログ信号からfsのクロックごとに切り出されると書きましたが、この後の処理に支障がないようにするには切り出されたデータと同じタイミングでこの後も処理をしていく必要があります。これは機器内部の話だけでなく機器間でデータを受け渡しする場合も同様で、これがズレると次の段階へのデータの受け渡しが滞ったり隙間が空いたりして支障が出てしまいます。具体的には音が途切れたりデータエラーによるノイズが発生したりします。
オーディオ機器の場合、このタイミングを取り仕切っているのがワードクロック(以下、WC)で、すべての処理がこのWCを基準に行なわれます。これを同期といいます。当然ながらfsもWCから作られます。
ここで重要なのがWCの正確さです。正確さとは周波数の正確さとゆらぎの少なさです。ゆらぎは正式にはジッター(Jitter)と呼ばれます。これらが重要になるのはWCでロックされているひとつのシステム内では当然ですが、特に録音再生する場合です。記録される時のWC周波数と、再生する時のそれが違うと再生された音そのもののピッチが変わってしまいますし、正確なWCで記録されたデータでも再生システムのWCにゆらぎが多いと正確な波形が再現できません。別の言い方をすると、アナログをデジタル化するADCパートにこそ最も正確なWCが必要ということで、その後でいかに正確なWCが使用されたとしても最初の歪みやゆらぎは残ったままになりますからね。
また1サンプルのデータの中身も同じで、16bitの場合1サンプルは16個の0か1で構成されていますが、この0と1についても規則的に送らなければなりません。この時に使用されるのがビットクロックです。当然このビットクロックもWCから作られます。
これらのクロックがズレると実際にどのようになるかを図1で説明しましょう。これはビットクロックの例です。全く違うデータになってしまうのがお分かりいただけると思いますが、違うデータになる=ノイズになることも含めて元とは違う音になる、ということなのです!
※2:WCは電気信号ですが無限のスピードを持っているわけでありません。しかも同軸ケーブルの中では通常よりもスピードがかなり落ちます。例えば伝送スピードが250,000km/s とすると96kHzの WCの1波長は2,600mですから10m伝送すると 1.4°位相が遅れます。厳密に言うと、この位相の遅れはクロックのズレになりますので、WCの配線はマスター機から同じ同軸ケーブルを等長で配線するのがベストです。ただ、最近の機器にはWCの遅延補償機能があるので昔のように神経質にならなくても良いようです。
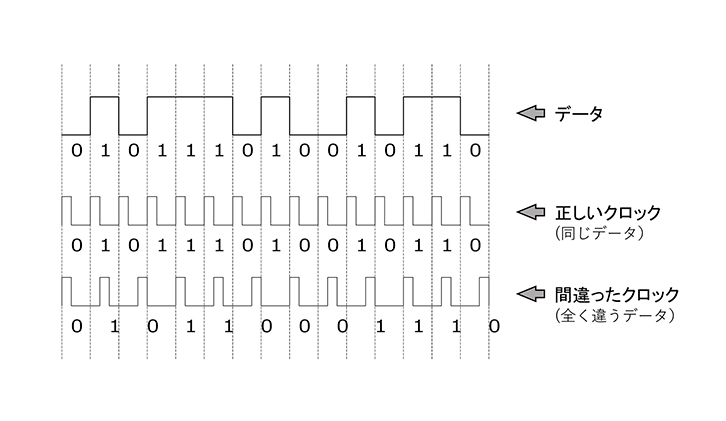
図1 クロックずれが起きるとどうなるか?
これは極端な例だが、まったく違うデータとなってしまう
FIRって何?(1)
早速FIRという言葉が登場しましたが、ここではまだ触りだけ、詳しくは第2回目でご説明します。
FIRは英語のFinite Impulse Responseの頭文字を取ったものです。日本語では「有限インパルス応答」と訳されます。頭に「有限」が付いていますが、「有限」があるなら「無限」があるの?…という疑問を持たれた方もおられると思います。はい!これがあるのです!「無限インパルス応答」これを英語にするとInfinite Impulse Response。略して「IIR」。実はこれ従来のEQのことなのです。もちろん、デジタルで信号を処理する時の演算方法のお話ですが、アナログと同じ特性のEQを作る時にはこのIIRを使います。
IIRとFIRの特徴の違いを纏めると表1のようになります。
この特徴の中でEQのバンド数のところを見てください。IIRは従来のEQの概念そのままですが、FIRではバンドという概念がありませんね。全体をひとつのEQカーブとして演算するからで、そこにはFrequency、Q、Gainという概念自体がないのです!ここが従来のEQと最も大きく異なるところです。では、何故ないのか? これこそが「超解説FIR!」の骨子になりますのですべて読み終わる頃には何となくご理解いただける…ハズです!
ところで、有限や無限の次に「インパルス応答」という言葉が出てきます。これって何でしょうか?
表1 IIRフィルターとFIRフィルターの違い
| IIRフィルター | FIRフィルター | |
|---|---|---|
| EQカーブの種類 | IIRフィルター アナログと同じ形 (HPF、LPF、ピーキング等) |
FIRフィルター 任意のカーブを作ることができる |
| EQによる遅延 | IIRフィルター 小さい |
FIRフィルター 位相設計法による 直線位相:大きい 最小位相:小さい |
| EQのバンド数 | IIRフィルター ひとつのIIRフィルターで1バンド (バンド数は任意に増やせるが必要な処理能力も増える) |
FIRフィルター 全体をひとつのカーブとして扱うのでバンドという概念がない (Frequency、Q、Gainという概念自体がない) |
| 必用ハードウェア規模 | IIRフィルター 小さい |
FIRフィルター 大きい |
インパルス応答って何?
アナログやデジタルに関わらず信号の処理を説明する、インパルス応答は非常に重要なファクターとなります。
皆さんはあるホールに行き、このホールはどんな響きかな?と思った時に手を叩きませんか? その時にどんな音がします?パンと手を叩く音がした後にその部屋の「響き」が聴こえますよね。この「響き」こそが私たちが最も身近に知ることのできるインパルス応答です(厳密にいうと少し違いますが、それは後述します)。
これを波形で見ると、図2のようになることはご存知の通りです。これはエネルギーが時間的にある測定点にどのように到達してきたかを示すもので、エコータイムパターンとも呼ばれます。
この図をよく見ると、一番初めにある大きなパルス状の波形は手を叩いた音そのものですが、その後の波形は空間によって新たに生み出されたもの(=反射音)です。言い替えれば「手を叩いた時のパルス音をあるホールというブラックボックスに入力した時、“響き”という応答があった」と考えることができます。つまりパルス音の応答ですね。ちなみに無響室で測ると最初のパルスだけしか現れません。
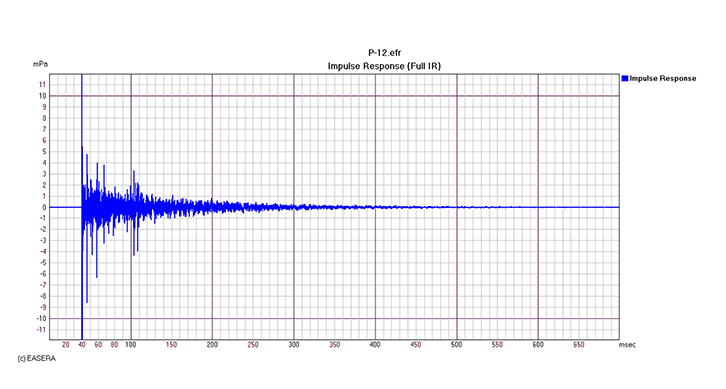
図2 エコータイムパターン
最初の大きなパルス以外の波は、そのパルスによってその空間の中で新たに起こった出来事を表している。つまりパルスによる応答
インパルスとは
手を叩いた時の音はパルス波形だと前述しました。パルスとは時間的に急激に変化する信号の総称ですが、その信号の幅をゼロにしたものがインパルスです。実際に手を叩いて出した音には幅がありますから厳密にいうとインパルスではありません。前項で「厳密にいうと違う…」と書いたのはそういった理由からです。また、理想的なインパルスとは幅がゼロで大きさ(波形の高さ)が無限大のものを差します。ただ「幅が0?」「大きさ無限大?」といわれても概念的に理解できませんよね。そこでもう少し分かりやすく説明したのが図3です。
同図Aを見てください。このように、ある一点だけが無限大でその他は0のものには名前が付いておりデルタ関数といいます。そしてこれを積分すると1となります。積分とは面積を求めることですからこのインパルスの面積が1ということです。何故かは積分のお話をしなければなりませんのでここでは省略します。
次に同図Bを見てください。これは幅がdtで高さが1/dtのパルスです。このパルスの面積はお分かりのようにdt×1/dtですからこれを計算すると=1ですよね。つまり積分値(面積)が1となります。この波形なら感覚的に分かりますね。このdtを限りなく0に近付けたものがインパルスです。
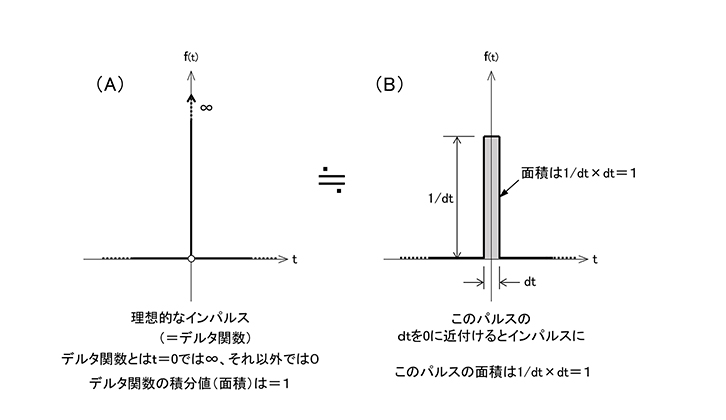
図3 インパルスとは? デルタ関数とは?
インパルスはすべての周波数成分を持っている
ここで図4を見てください。純音とはSIN(サイン)波またはCOS(コサイン)波のことですが、ある周波数の純音(基本波)とその整数倍の純音(高調波)を同じレベルで加えていくと基本波のピークのところが加算されて次第にレベルが高くなり、その両側は干渉して次第にレベルが小さくなっていきます。この高調波を無限に加えたものがインパルスです。
ということは、インパルスにはすべての周波数が同じレベルで含まれているということになりますね。また、図の左端をよく見ると整数の高調波と奇数の高調波は上から始まるものと下から始まるものが交互になっていますね。これは片方をSIN波とするともう片方はCOS波であることを意味しています。
このことを別の方法で説明しましょう。
ある波形からその周波数成分を分析することをフーリエ変換といいます。これをもう少し難しく表現するなら「ある波形の時間情報の中のある、ある時間のデータを周波数情報に変換する」となります。さらに別の言葉では時間積分するといいます。先ほどインパルスを積分すると1になるといいました。つまり、インパルスをフーリエ変換(時間積分)すると1になるのです。では1とはどういうことでしょうか? ある波形の周波数関数、例えばf(x)が1ということはグラフで書くとすべての値が1です。横軸は周波数ですからすべての周波数でY軸(大きさ)が1(=定数、一定の値)、つまり同じ大きさになるということです(図5)。このことからインパルス信号はすべての周波数成分を均等なレベルで持っているといえますが、これは先程の図4の説明と矛盾しませんね。
参考までに、ある周波数の純音にその奇数倍の高調波をそれぞれ1/N倍(N=3,5,7,…)のレベルで足し合わせると矩形波になり、また、整数倍の高調波をそれぞれ1/N倍(N=2,3,4,5,…)のレベルで足し合わせるとノコギリ波になります。ちなみに、ある波形からその成分を分析することをフーリエ変換すると説明しましたが、その分析通りに音を合成すると元の波形ができます。これを逆フーリエ変換といいます。実は初期のシンセサイザー(Moog!等)に使われていたのがこの原理なのです!
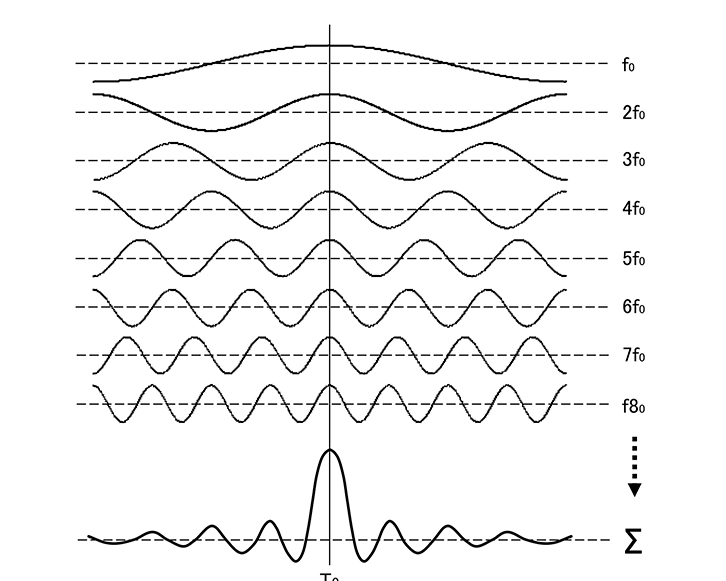
図4 インパルスはすべての周波数の集まり
このように同じ振幅で無限に周波数が重なると、中央だけが加算されて無限のエネルギーになり、それ以外は干渉して0となる=これがインパルス。このことからインパルスには全周波数成分が同じ振幅で含まれていることが分かる
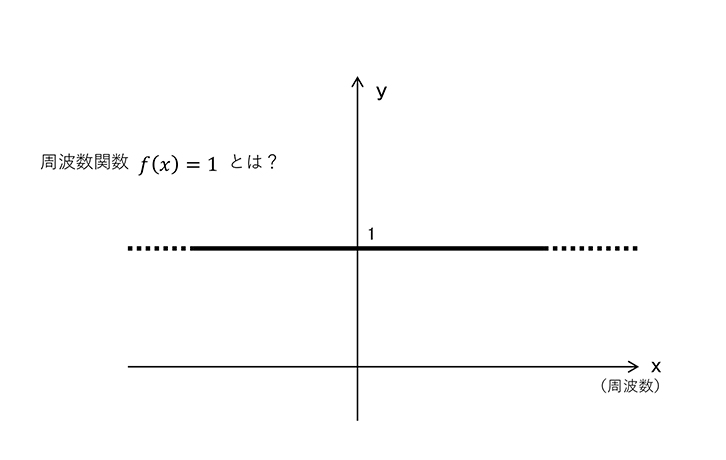
図5 波形の周波数関数が1とは
すべての周波数で同じ値(=1)、つまり全周波数が同じ量含まれている
群遅延
前述の通りインパルスはすべての周波数を同じエネルギー量(同じ振幅)含んでいますので、入力したそのインパルス信号の反応、つまりインパルス応答を周波数という軸で見る(=フーリエ変換する)と各周波数のエネルギーがどのように応答しているかが分かります。これが周波数特性ですね。また、各周波数が時間的にどのくらい遅れて到達しているかを見たものが位相特性になります。そして少し難しくなりますが、この位相を周波数で微分したものが群遅延特性です。微分とは変化量を表すものですから、周波数とその位相の変化量(遅れ)が比例していれば群遅延は一定(直線)となります。
では、微分などと言わずにこの群遅延をもう少し分かりやすく説明しましょう。図6を見てください。今1msec.の遅れがあるとします。この遅れは1kHzでは1波長の遅れですが、2kHzでは2波長の遅れになり、10kHzでは10波長の遅れになります。このように周波数に対して規則正しく遅れていく状態を「群遅延が一定」といいます。一定でない部分があるとそれは位相がズレる、または歪むということになります。よく“位相ひずみがある”などと言われるのは、この現象です。現実的にアナログの世界ではこの群遅延が一定になることはありません。しかしデジタルの世界ではある条件下で可能になります。それは次号までしばしお待ちを。
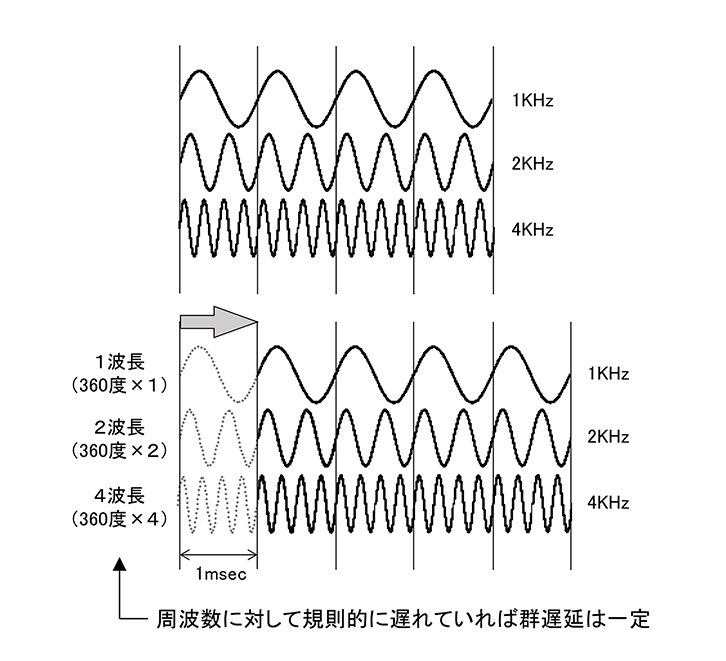
図6 群遅延とは
周波数に応じて位相が「比例して変化」していれば群遅延は一定となる。
インパルス応答、周波数特性、伝達関数は同じもの
皆さんは伝達関数という言葉に聞き憶えがあることと思います。これはある信号をブラックボックスに入力した時、その入力に対してどのような出力が出てきたかを表したものですが、このブラックボックスにインパルスを入力した時に出力された信号がインパルス応答ですね。
いま、ひとつのブラックボックスがあるとします。そこにインパルスを入力します。入力された信号はすべての周波数を同じエネルギー量持っているインパルスですから、この出力信号であるインパルス応答を見ただけでブラックボックスの中身、つまりどのような伝達関数を持っているかが分かります。言い方を変えると、インパルス応答は伝達関数と同じことですよね。また、前述の通りこのインパルス応答を周波数の観点で見ると周波数特性が分かり、周波数ごとの到達時間を調べれば位相特性が分かります。つまりインパルス応答、伝達関数、周波数特性、位相特性等はひとつのデータの見方を変えただけで同じものだということが分かります。「Smaart®」や「Systune®」でインパルス応答を測っただけで周波数特性や位相特性が出てくるのはこのような理由からです。
デジタルフィルターのインパルス応答
では実際のインパルス応答と周波数特性の関連を見てみましょう。図7からインパルス応答が周波数特性のカーブになることが分かりますが、別の見方をすると、周波数特性=EQカーブを作りたければそのインパルス応答波形を作ってやれば良いのです。実はデジタルEQはそれをやっているのです! ですからデジタルフィルターについての考察は、いかにして目的のインパルス応答波形を作るかに繋がるお話なのです。
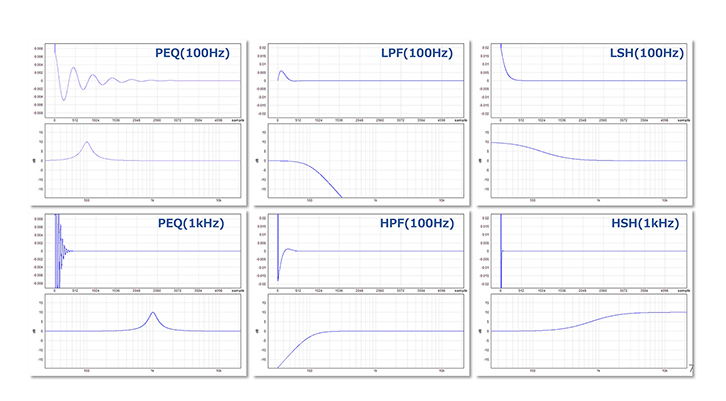
図7 インパルス応答と周波数特性
左端の上下2つは同じピーキング特性で周波数を変えたもの(本文参照)
インパルス応答の長さ
もう一度、図7を見てください。EQカーブの違いによりインパルス応答の形や長さが変わることが分かりますが、左端の2つの波形を見比べてください。これは共にピーキングEQをした時の波形ですが、これらは周波数が違っているのが分かりますね。今度はそのインパルス応答波形を見比べてください。違いが見えますか? そう、応答の長さが違います。高い周波数に比べて低い周波数はインパルス応答の長さが長くなっています。FIRではこの長さの違いが重要になります。実はFIRでは扱える長さに限界があります。それが「有限」の理由です。
長さは図の通り最低周波数=周波数解像度を表していますが、この長さの限界に関連する言葉がTap(タップ)数です。
詳しくは次回お話ししますが、
fs(サンプリング周波数)÷Tap数=周波数解像度
となります。例えばfs=96kHz、1024Tapの場合、この計算式を当てはめると周波数解像度は≒94Hzとなります(96000Hz÷1024=93.75Hz)。周波数解像度とは扱える最低周波数ということですが、「解像度」ですので94Hzの次は188Hzとなります。お分かりのようにこれでは120Hzや130Hzを操作することができません。それならTap数を増やせば良いのでは?と考えますよね。当然それで解像度を小さな値にすることも可能です。例えば10倍の10240Tapにすれば周波数解像度は9.4Hzとなりますので何とかいけそうです。しかしそこには大きな問題が!
……次号へ続く。
●
本誌で私が連載をしております「プロサウンド的“設備”検分録」同様、本連載でもご質問を受け付けています。どのような内容でも構いません。下記に示すメールアドレスまでご送信ください。「超解説FIR!」は全3回に分けて別表(P.80)のようなカリキュラムで展開する予定ですが、もしこれらの内容以外にもリクエストがございましたら、次号以降の内容にも反映していきたいと思っております。皆さまからのメールをお待ちしています!
筆者紹介 --------------------------
三村美照(みむら・よしてる)
音響システム設計コンサルタント。1978年「スタジオサウンドクリエーション」に入社、レコーディング・エンジニアとして経験を積む。その後、業務用音響機器の設計業務を経て、1989年から本格的に音響システム設計に従事、現在「M&Hラボラトリー」代表取締役を務める。仕事においては「ベストではなくベター、ベストとは逆に「終わり」を意味する。私たちの仕事に終わりはない」、「常により良いものを、よりシンプルに」をポリシーに「設備の音」を築き続けている。長居陸上競技場、新広島球場、サンケイホール、大阪フェスティバルホール、国立京都国際会議場、新神戸国際会館等をはじめ実 績例は100件以上と多岐多数
Copyright © 2024 Yamaha Sound Systems Inc. All Rights Reserved.